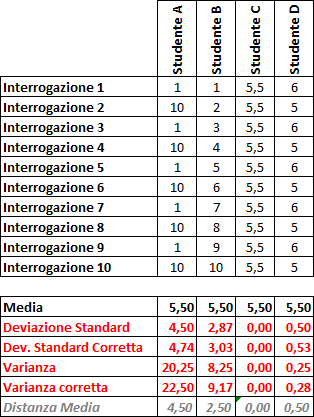
Immaginiamo di avere 4 studenti con i seguenti voti:

Tutti è 4 gli studenti hanno la medesima media ma la variabilità nei voti conseguiti è decisamente differente. Se raffiguro il comportamento dei singoli voti in un grafico ottengo le seguenti rappresentazioni:
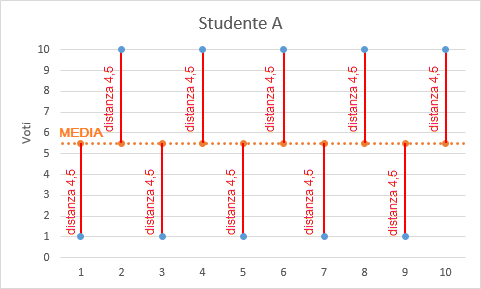
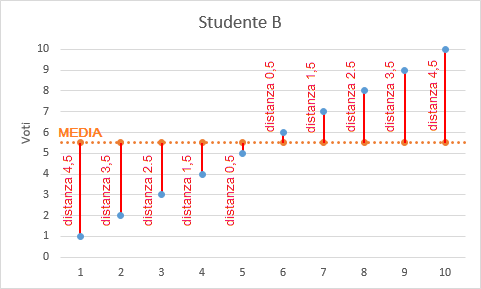
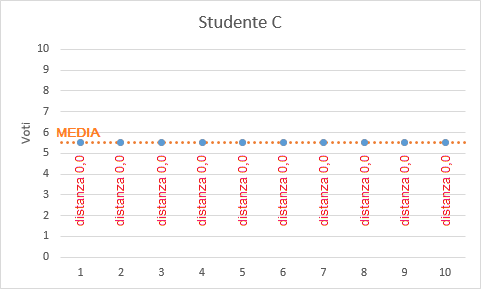
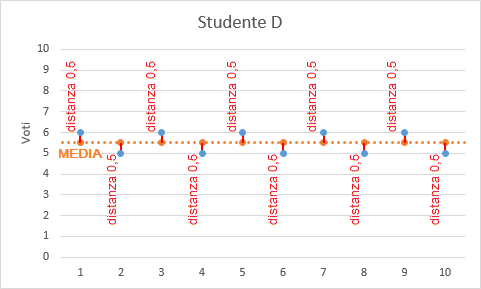
Il grafico evidenzia i diversi comportamenti delle singole sequenze di voti dove la differente variabilità può essere riferita ad uno studio non continuativo oppure a livelli di difficoltà nelle verifiche differenti (in questo caso è possibile evidenziarli analizzando le medie e le varianze delle singole verifiche assegnate ad una classe).
Maggiore è la variabilità di un fenomeno e minore sarà il suo grado di prevedibilità. Diventa quindi importante avere un indicatore che misuri lo scostamento medio della sequenza rispetto ad un indice di posizione come ad esempio la media.
La distanza media dei valori xi della sequenza X rispetto alla loro media aritmetica M può essere considerato un indice che ci consente di misurare il grado di variabilità della sequenza.
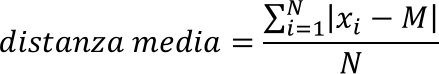
In realtà in statistica la variabilità viene generalmente valutata mediante altri indicatori ed esattamente:
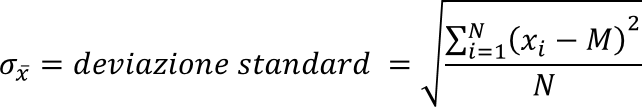
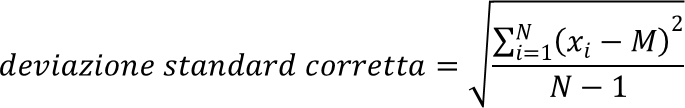
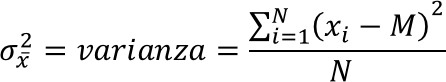
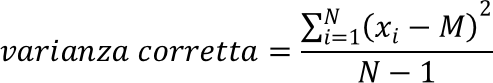
dove M è la media aritmetica degli N valori xi della sequenza X.
Con questi indici è possibile valutare la dispersione statistica (ovvero stimare la variabilità) di una popolazione di dati o di una variabile casuale rispetto ad un indice di posizione come ad esempio la media aritmetica o una sua stima. Si osservi che la deviazione standard (nota anche come scarto quadratico medio) è la radice quadrata della varianza.
Si può dimostrare che la deviazione standard può essere calcolata facendo la radice quadrata della differenza tra la media dei quadrati dei valori della sequenza xi e il quadrato della loro media M:
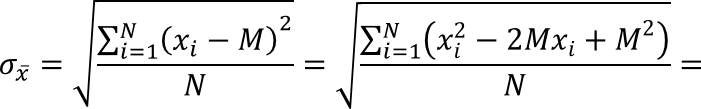
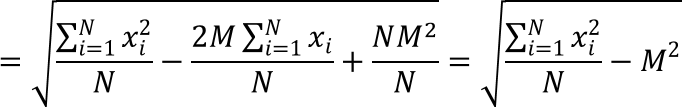
Le stime relative alla variabilità dei voti dei 4 studenti iniziali diventano: