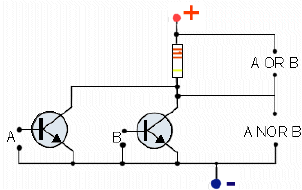
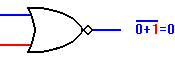
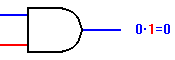
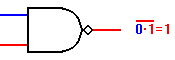
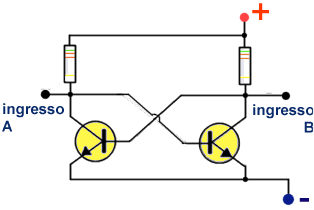
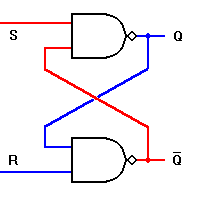
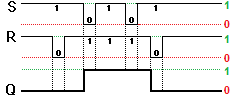
Il circuito evolve in accordo con le seguenti specifiche:
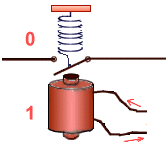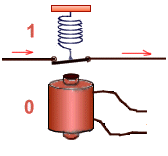
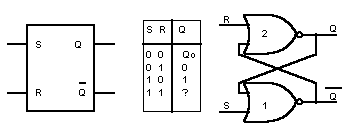
1) quando lo stato d'ingresso è S=0 e
R=1 il flip-flop si setta, cioè porta a 1 il valore
della variabile d'uscita Q;
2) quando lo stato d'ingresso è S=1 e
R=0 il flip-flop si resetta cioè porta a 0 il
valore della variabile d'uscita Q;
3) quando lo stato d'ingresso è S=1 e
R=1 il flip-flop conserva, cioè mantiene inalterato
il valore di entrambe le variabili d'uscita. Quindi quando entrambi i valori R e
S sono alti, il flip-flop si trova nello stato neutro e mantiene il valore
delle uscite, ovvero si dice che "fa memoria" (mantiene cioè in uscita il dato
precedente memorizzato).
4) Quando invece entrambi gli ingressi hanno valore 0, si ha
Q e
Q entrambe a 1. Tale
combinazione è considerata proibita nel Flip-Flop RS.
La condizione Set significa che viene disposto l'output Q a 1. In modo analogo,
la condizione reset significa ridisporre (cancellando) l'output
Q a 0
Flip-flop sincronizzati
Spesso l’eventuale cambiamento di stato di un flip-flop non si fa coincidere con
l’istante in cui si modificano i valori dei bit di ingresso ma con l’istante in
cui un ulteriore ingresso, detto ingresso di sincronismo o ingresso di clock e
denominato con la sigla CK, va da 1 a 0 oppure da 0 a 1.
Un flip-flop che funziona col clock prende il nome di flip-flop sincronizzato.
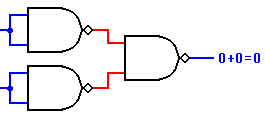
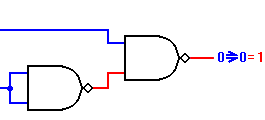
I flip-flop esaminati nelle figure 1e 2, invece, essendo privi di ingresso di
clock, sono denominati flip-flop Set Reset asincroni.
Il flip-flop si dice attivo sul livello quando il clock è caratterizzato da un
livello logico (0 o 1) applicato all'omonimo ingresso.
Il flip-flop si dice attivo su fronti (edge triggered) quando l'eventuale
modifica dello stato di uscita dipende dal fronte positivo o di salita (PET =
Positive Edge Triggered) o dal fronte negativo o di discesa (NET = Negative Edge
Triggered).
Sui dice, anche, che l'uscita si aggiorna nel:
PET quando il clock passa da 0 a 1;
NET quando il clock passa da 1 a 0.
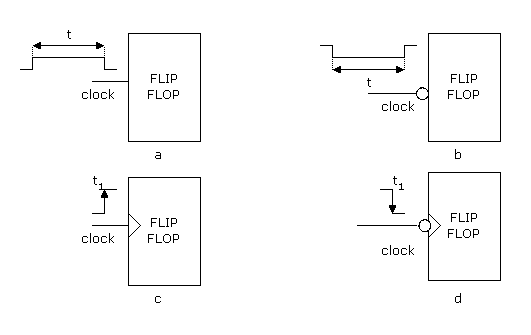 |
Fig.3 - Flip-flop sensibili ai livelli ed
alle transizioni.
Il flip-flop "a" è sensibile al livello logico 1 e funziona
nell'intervallo di tempo t.
Il flip-flop "b" è sensibile al livello logico 0 durante il tempo t.
Il flip-flop "c" è di tipo PET e funziona solo nell'istante t1.
Il flip-flop "d", infine, è di tipo NET e funziona solo nell'istante t1. |
Flip-flop S-R sincronizzato
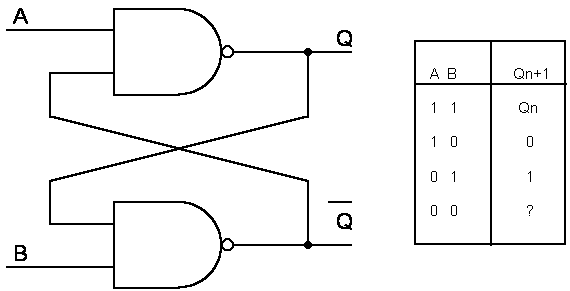
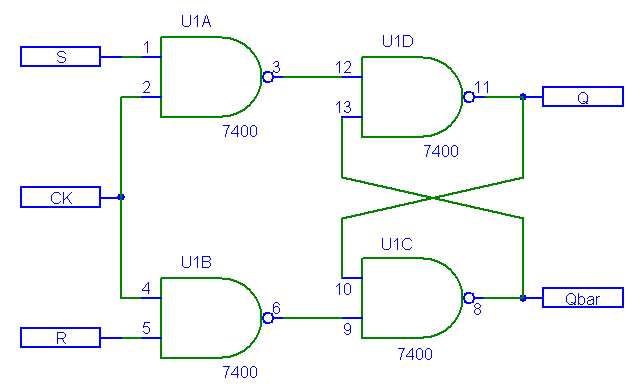
In fig.4 si mostra lo schema logico del flip-flop Set Reset sincronizzato. Esso
è costituito da due porte logiche NAND, dette porte pilota, e da altre due porte
NAND che realizzano il flip-flop S R vero e proprio del tipo mostrato nella
precedente fig.2.
Se il clock CK è al livello logico 1 le porte pilota si comportano da NOT e
quindi gli ingressi S ed R sono effettivamente coincidenti con gli omonimi
ingressi del generico flip-flop Set Reset.
Se, invece, il clock CK è al livello logico basso, le uscite delle due porte
pilota sono al livello logico 1 indipendentemente dai valori applicati agli
ingressi S e R. Per tale combinazione la "latch" a porte NAND conserva lo stato
precedente e quindi il flip flop è insensibile ai comandi esterni applicati.
Nella tabella della verità si riporta l'uscita futura Qn+1 in funzione del
clock, degli ingressi S ed R e dallo stato presente Qn.
X rappresenta indifferentemente sia lo stato logico 0 che lo stato logico 1.
|
CK |
S |
R |
Qn |
Qn+1 |
|
0 |
X |
X |
0 |
0 |
|
0 |
X |
X |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
da evitare |
|
Fig.4. - Flip-flop SR sincronizzato con
porte NAND.
U1A e U1B costituiscono le porte pilota.
Le porte U1C e U1D rappresentano il flip-flop vero e proprio.
Con Qbar si indica l'uscita Q (Q
barrata). |
Flip-flop JK
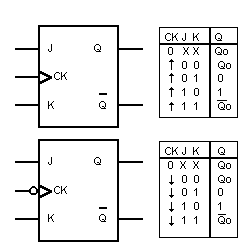
Il flip-flop JK è un dispositivo a due entrate denominate J e K che operano in
modo analogo alle entrate S ed R di un flip-flip Set Reset con la differenza che
se : J=1 e K=1 l’uscita commuta, cioè se lo stato presente è 0, lo stato futuro
è 1 e viceversa.
Per evitare commutazioni multiple, nel caso si lasci a lungo la combinazione J=1
e K=1, tale flip-flop deve essere necessariamente sincronizzato.
 |
|
J |
K |
Qn |
Qn+1 |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
Flip-flop JK e tabelle della verità. A
destra si mostra la tabella della verità che prescinde dalla presenza
del clock e che mostra l'uscita futura in presenza degli ingressi
esterni J e K e dallo stato presente Qn. |
In fig.5 si mostrano due flip-flop JK sincronizzati. Il primo adegua le uscite
quando al clock si applica un segnale digitale che passa da 0 a 1 (transizione
positiva indicata con una freccia verso l’alto nella tabella della verità). Il
secondo adegua le uscite quando al clock si applica un segnale digitale che
passa da 1 a 0 (transizione negativa indicata con una freccia verso il basso
nella tabella della verità).
Il primo flip flop JK si dice di tipo PET (Positive Edge Triggered), il secondo,
invece, si dice di tipo NET (Negative Edge Triggered).
I flip-flop JK si realizzano con una soluzione circuitale costituita da porte
logiche secondo uno schema interno più complesso rispetto a quello visto per il
flip-flop SR realizzato a porte NOR e a porte NAND.
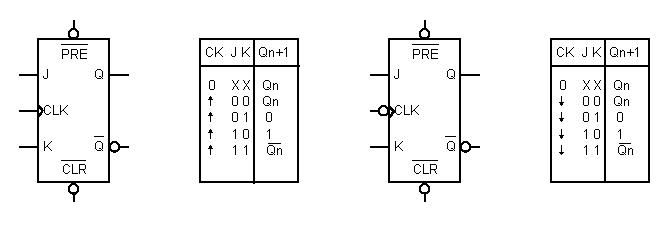
Si mostrano, in fig.6, i simboli logici e le tabelle della verità di due diversi
flip-flop JK, il primo di tipo PET ed il secondo di tipo NET, con ingressi
asincroni di preset (PRE) e di clear (CLR).
 |
|
Fig.6 - Simbolo del flip-flop JK PET e
relativa tabella della verità ( a sinistra);
simbolo del flip-flop JK NET e relativa tabella della verità ( a
destra).
Si noti il simbolo del clock nei due casi.
La maggior parte dei flip-flop integrati presentano, inoltre, ingressi
asincroni di preassegnazione a 1 (PRE) e/o di azzeramento (CLR clear).
Quelli indicati in figura sono attivi bassi: se, ad esempio, si applica
un livello logico basso sulla linea PRE, il flip-flop memorizza 1
indipendentemente dal clock; se, invece, si applica un livello logico
basso sulla linea CLR, il flip-flop memorizza 0 indipendentemente dal
clock. |
Flip-flop D
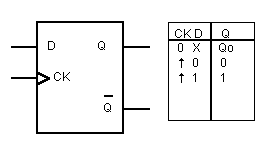
Presenta un solo ingresso denominato D. Spesso è di tipo sincronizzato e
funziona nel seguente modo: quando è attivo l’ingresso di clock l’uscita assume
lo stesso valore applicato all’ingresso D. In assenza di comando di clock
l’uscita conserva lo stato precedente indipendentemente dal valore applicato
all’ingresso D.
In fig.7 si mostra il simbolo logico e la tabella della verità del flip –flop D.
Il flip-flop D rappresenta l’elemento fondamentale delle memorie centrali degli
elaboratori ( almeno a livello concettuale).
Flip-flop T
E' un flip-flop avente una sola entrata denominata T e le solite due uscite: Q e
la sua complementata Q.
L'uscita Q conserva lo stato precedente se T=0 e commuta se T=1 quando si
applica il segnale di clock.
I flip-flop T, al contrario dei JK, D e SR, non sono disponibili commercialmente
in forma integrata poiché si possono ottenere direttamente dai flip-flop JK
semplicemente collegando tra loro gli ingressi J e K.
E' utilizzato come dispositivo divisore di frequenza di clock per due e nei
contatori digitali.
Si mostra in fig.8 il collegamento di un flip-flop NET di tipo JK per ottenere
un flip-flop di tipo T e la relativa tabella della verità.
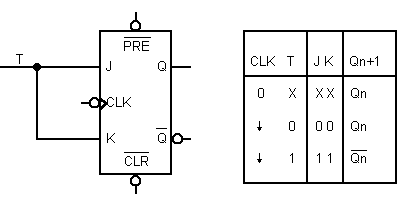 |
Fig.8 - Simbolo del flip-flop T e relativa tabella
della verità.
Dalla tabella si nota che solo quando il clock passa dal livello logico
alto al livello logico basso si ha:
Qn+1=Qn se
T=0 e Qn+1=Qn
se T=1. |
per approfondire vedere:
http://digilander.libero.it/panetti/digitale/flip_flop.htm |