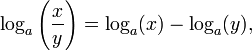Logaritmo

Alcune ipotesi su a e x sono necessarie per ottenere una buona definizione di y. Infatti:

• Se a = 0 e x<>0, non esistono y tali che x = a^y.
• Se a = 0 e x = 0, esistono infiniti y tali che x = a^y.
• Se a = 1 e x<>1, non esistono. (Non esiste nessun numero che possa essere ottenuto attraverso una potenza di 1. Infatti 1 elevato a qualunque numero dà sempre uno).
• Se a = 1 e x = 1, ne esistono infiniti. (Possiamo elevare 1 a qualsiasi numero ma otterremo sempre 1).
• Se a < 0, l'elevamento a potenza a^y non è definito per tutti i numeri reali y (può essere definito solo sui naturali e in generale sui razionali esprimibili con una frazione con denominatore dispari).
• Il risultato di un elevamento a potenza (di un numero positivo, per l'osservazione precedente) è un numero positivo, quindi deve essere x > 0.

Proprietà dei logaritmi

• Il logaritmo in base a di a è 1:

• Il logaritmo di 1 è, in qualsiasi base, 0:

 

• Vale l' identità:

• Il logaritmo del prodotto di due numeri è uguale alla somma dei logaritmi dei due numeri:

Cambio di base:

Noto il valore di un logaritmo in una base, è semplice calcolarne il valore in un'altra base (spesso le calcolatrici danno il logaritmo solo in basi 10 ed e).
Se b, x, e k sono tutti numeri reali positivi (con b ≠ 1 e k ≠ 1):

dove k è una base qualsiasi. La formula può essere scritta nel modo seguente

e segue dalla relazione

Dalla formula del cambiamento di base, ponendo k = x, si ricava la relazione seguente:

un valore che ci sarà molto utile è

Nelle notazioni in Floating Point appare sempre una potenza di 2. Per passare dalla floating point

(parte normalizzata in base 2) x 2 ^esponente

a quella in base 10 può essere utile valutare il 2^x in potenza di 10 tenendo presente che:

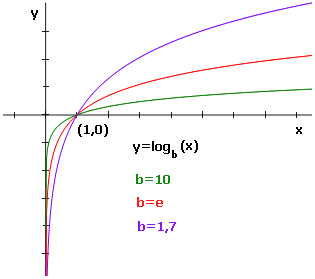
Funzione logaritmo