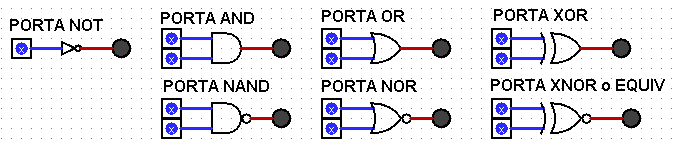

| ESERCIZIO 2.1 |
Calcola il risultato delle seguenti espressioni booleane
| 1 | (True AND False) OR NOT False | (True
AND False) => False NOT False => True quindi False OR True => True |
| 2 | (True XOR False) XNOR True | |
| 3 | (True OR False) AND False | |
| 4 | (True AND False) OR (False EQUIV False) | |
| 5 | (False NAND False) NAND (True NAND False) | |
| 6 | (True XNOR False) XNOR False | |
| 7 | NOT True NOR (False XOR False) | |
| 8 | True AND True AND True AND False | |
| 9 | (False OR True) XOR NOT (False NAND True) | |
| 10 | (False OR (True XOR NOT False)) NAND True |
| ESERCIZIO 2.2 |
Rappresentare, utilizzando il simbolismo delle porte logiche, le seguenti espressioni booleane
| 1 | (A AND B) OR NOT C |
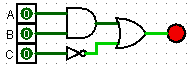 |
| 2 | (A XOR B) XNOR C | |
| 3 | A OR B AND C | |
| 4 | A AND (B OR (C EQUIV D)) | |
| 5 | (A NAND B) NAND (C NAND D) | |
| 6 | (A XNOR B) XNOR C | |
| 7 | NOT A NOR (B XOR C) | |
| 8 | A AND B AND C AND D | |
| 9 | (A OR B) XOR NOT (C NAND D) | |
| 10 | (A OR (B XOR NOT C)) NAND D |