| ESERCIZIO 1 (FOR) |
Costruire un programma che dopo aver chiesto un intero n calcoli la somma Sn dei primi n numeri interi
Sn=1+2+3+.. +(n-1)+n
def is_integer?(object)
object.to_i.to_s == object.to_s
end
print "Digita un intero n: "
n=gets.chomp
if (is_integer?(n)) then
s=0
for i in 0..n.to_i
s=s+i
end
print "S(#{n})=#{s}"
else
print "Non hai digitato un valore intero!"
end
Il ciclo for poteva essere implementato anche in questo modo:
for i in Array(0..n.to_i) # Scorre gli elementi di un array
s=s+i
end
Array(0..n.to_i).each { |i| s=s+i } # Scorre gli elementi dell'array ...
# oppure
(0..n.to_i).to_a.each { |i| s=s+i }
# oppure
(0..n.to_i).to_a.each do |i|
s=s+i
end
(n.to_i+1).times { |i| s=s+i } # ripete n volte un'operazione ...
# oppure
(n.to_i+1).times do |i|
s=s+i
end
0.upto(n.to_i) { |i| s=s+i } # da 0 a n esegue ...
# oppure
0.upto(n.to_i) do |i|
s=s+i
end
0.step(n.to_i,1) { |i| s=s+i } # da 0 a n con passo 1 esegue ...
# oppure
0.step(n.to_i,1) do |i|
s=s+i
end
| ESERCIZIO 2 (FOR) |
Costruire un programma che richiede un intero positivo n e un valore reale (float) x e successivamente calcola, in modo iterativo, la potenza xn.
xn=x*x*...x
def is_integer?(object)
object.to_i.to_s == object.to_s
end
def is_number?(object)
true if Float(object) rescue false
end
print "Digita un intero n: "
n=gets.chomp
print "Digita la base x: "
x=gets.chomp
if (is_integer?(n) && is_number?(x)) then
n=n.to_i
x=x.to_f
p=1
for i in 1..n
p=p*x
end
puts "#{x}^#{n} = #{p}"
else
print "I valori non soddisfano i requisiti richiesti!"
end
| ESERCIZIO 3 (FOR) |
Costruire un programma che legge un intero n e restituisce il fattoriale n!
n!=1*2*:..*(n-1)*n
def is_integer?(object)
object.to_i.to_s == object.to_s
end
print "Digita un intero n: "
n=gets.chomp
if is_integer?(n) then
n=n.to_i
f=1
for i in 1..n
f=f*i
end
puts "#{n}! = #{f}"
else
print "Non hai digitato un intero!"
end
| ESERCIZIO 4 (FOR) |
Costruire un programma che legge un intero n e genera i primi n termini della sequenza di Fibonacci
x1, x2, x3 ... xn-2, xn-1, xn
dove il termine i-esimo xi è così definito:
x1=1
x2=1
xn=xn-1+xn-2
(nel nostro caso la sequenza sarà 1, 1, 2, 3, 5, 8, 13, ...)
print "Dammi n: "
n=gets.to_i
x1=1
x2=1
puts "x_1=#{x1}"
puts "x_2=#{x2}"
for i in 3..n
x3=x1+x2
puts "x_#{i}=#{x3}"
x1=x2
x2=x3
end
| ESERCIZIO 5 (FOR) |
Costruire un programma che genera una sequenza di n numeri con decimali (n è richiesto all'utente). Al termine della lettura il programma mostra la lunghezza della sottosequenza crescente più lunga.
print "Dammi n: " # Leggo la lunghezza della sequenza n=gets.to_i rnd=Random.new(Random.new_seed) # inizializzo il generatore di numeri casuale pi=1 pf=1 maxSeq=0 # massima lunghezza sottosequenza nrSeq=0 # lunghezza iniziale sottosequenza xp=0 # valore fittizio di start pi_max=pi pf_max=pf for i in 1..n xa=rnd.rand(1.0..10.0) # genera un float in [1.0,10.0] print "#{"%.2f" % xa}; " # stampa l'iesimo numero print "\n" if i % 10 ==0 if (xp<xa) nrSeq=nrSeq+1 pf=i else if nrSeq>maxSeq maxSeq=nrSeq pi_max=pi pf_max=pf end nrSeq=1 pi=i pf=i end xp=xa end if (n>0) if nrSeq>maxSeq maxSeq=nrSeq pi_max=pi pf_max=pf end print "\nMassima sequenza strettamente crescente: #{maxSeq} - dal #{pi_max}^ numero al #{pf_max}^ numero" end
| ESERCIZIO 6.a (FOR) |
Costruire una breve applicazione che partendo da un intero n generi i primi n termini della sequenza composta dal numero 1 con segno alterno ovvero:
1, -1, 1, -1, 1 ... (-1)n+1
La lunghezza n della sequenza deve essere richiesta all'utente
print "Digita n:" n=gets.to_i segno=1 for i in 1..n print segno.to_s + "; " segno=-segno end
| ESERCIZIO 6.b (FOR) |
Costruire una breve applicazione che partendo da un intero n generi i primi n termini della sequenza che ciclicamente propone 1, 0, -1. Ad esempio per n=7 la sequenza che verrà visualizzata sarà la seguente:
1, 0, -1, 1, 0, -1, 0
La lunghezza n della sequenza deve essere richiesta all'utente
print "Digita n:"
n=gets.to_i
for i in 1..n
if (i % 3) == 1
print "1, "
elsif (i % 3) == 2
print "0, "
elsif (i % 3) == 0
print "-1, "
end
endoppure
print "Digita n:"
n=gets.to_i
x=1
for i in 1..n
print "#{x} "
x=x-1
x=1 if (x==-2)
end
| ESERCIZIO 6.c (FOR) |
Costruire un programma che visualizza la progressione aritmetica di ragione 1 a segni alterni ovvero:
1, -2, 3, -4, 5 ... n*(-1)n+1
La lunghezza n della sequenza deve essere richiesta all'utente
print "Digita n:" n=gets.to_i for i in 1..n print ((-1)**(i+1)*i).to_s + "; " endoppure
print "Digita n:" n=gets.to_i segno=1 for i in 1..n print (i*segno).to_s + "; " segno=-segno end
| ESERCIZIO 6.d (FOR) |
Costruire una breve applicazione che legge un intero n e restituisce i primi n termini della sequenza composta dalla successione dei simboli: "A" "B" "C" "D" ed "E". Ad esempio per n=9 la sequenza che verrà visualizzata sarà la seguente
A, B, C, D, E, A, B, C, D
La lunghezza n della sequenza deve essere richiesta all'utente
print "Digita n:" n=gets.to_i for i in 1..n if (i % 5) == 1 print "A; " elsif (i % 5) == 2 print "B; " elsif (i % 5) == 3 print "C; " elsif (i % 5) == 4 print "D; " elsif (i % 5) == 0 print "E; " end endoppure
print "Digita n:" n=gets.to_i s="ABCDE" for i in 1..n print s[(i-1) % 5] +"; " end
| ESERCIZIO 7 (FOR) |
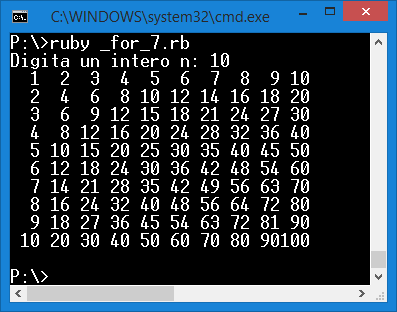
Costruire un programma che visualizzi la tavola pitagorica nxn. Il valore n è richiesto e deve essere un numero intero compreso tra 5 e 25 (in caso contrario verrà dato un avviso di errore).

def is_integer?(object)
object.to_i.to_s == object.to_s
end
print "Digita un intero n: "
n=gets.chomp
if (is_integer?(n)) then
n=n.to_i
if (n>=5 && n<=25)
for r in 1..n
for c in 1..n
v=r*c
print "#{"%3d" % v}"
end
print "\n"
end
else
print "La dimensione #{n} non e' valida - programma terminato"
end
else
print "Non hai digitato un valore intero!"
end
| ESERCIZIO 8 (FOR) |
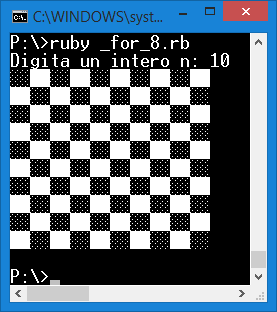
Costruire un programma che visualizza una scacchiera n x n dove la dimensione n è richiesta all'utente. Il valore n deve essere un numero intero compreso tra 5 e 25. Per stampare i caratteri speciali ▓▓ e ▒▒ si utilizzino le stringhe "\u2588\u2588" e "\u2591\u2591".
print "Digita un intero n: "
n=gets.to_i
if (n>=5) && (n<=25)
for r in 1..n
for c in 1..n
if (r+c) % 2 ==0
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n" # va a capo dopo aver stampato la riga
end
else
print "Out of range - 5..25"
end
| ESERCIZIO 9.0 (FOR-IF) |
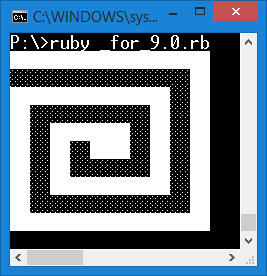
Costruire un programma che calcoli, nella tavola pitagorica 10x10, la somma dei numeri posizionati lungo la spirale evidenziata in azzurro. Suggerimento: analizzare lo script che disegna invece tale spirale.
|
 |
$N=10
def distanza(r, c)
# Guardo la minima distanza dal bordo
d = r - 1
d = (d > c) ? c - 1 : d
d = (d > ($N - c)) ? $N - c : d
d = (d > ($N - r)) ? $N - r : d
return d
end
for r in 1..$N
for c in 1..$N
if distanza(r,c) % 2 ==0
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabella 0 |
$N=10
def distanzaMod(r, c)
# Guardo la minima distanza dal bordo
d = r - 1
d = (d > c) ? c - 1 : d
d = (d > ($N - c)) ? $N - c : d
d = (d > ($N - r)) ? $N - r : d
return d
end
s=0
for r in 1..$N
for c in 1..$N
if distanzaMod(r,c) % 2 ==0
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}"
| ESERCIZIO 9.A.1 e 9.A.2 (FOR-IF) |
Costruire un programma che calcoli, nella tavola pitagorica 10x10, la somma dei numeri posizionati:
(Attenzione: non è richiesta la visualizzazione della tabella!)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabella 1 | Tabella 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SOLUZIONE
|
SOLUZIONE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
$N=10
s=0
for r in 1..$N
for c in 1..$N
if r==c || (r+c)==($N+1)
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
$N=10
s=0
for r in 1..$N
for c in 1..$N
if r==$N/2 || c==$N/2 || r==($N/2+1) || c==($N/2+1)
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
| ESERCIZIO 9.B.1 e 9.B.2 (FOR) |
Costruire un programma che calcoli, nella tavola pitagorica 10x10, la somma dei numeri posizionati:
(Attenzione: non è richiesta la visualizzazione della tabella!)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabella 1 | Tabella 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SOLUZIONE
|
SOLUZIONE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
$N=10
s=0
for r in 1..$N
for c in 1..$N
if r<=c
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
$N=10
s=0
for r in 1..$N
for c in 1..$N
if (r+c)>=($N+1)
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
| ESERCIZIO 9.C.1 e 9.C.2 (FOR-IF) |
Costruire un programma che calcoli, nella tavola pitagorica 10x10, la somma dei numeri posizionati:
(Attenzione: non è richiesta la visualizzazione della tabella!)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabella 1 | Tabella 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SOLUZIONE
|
SOLUZIONE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
$N=10
def distanza(r, c)
# Guardo la minima distanza dal bordo
d = r - 1
d = (d > (c - 1)) ? c - 1 : d
d = (d > ($N - c)) ? $N - c : d
d = (d > ($N - r)) ? $N - r : d
return d
end
s=0
for r in 1..$N
for c in 1..$N
if distanza(r,c)==0
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
$N=10
def distanza(r, c)
# Guardo la minima distanza dal bordo
d = r - 1
d = (d > (c - 1)) ? c - 1 : d
d = (d > ($N - c)) ? $N - c : d
d = (d > ($N - r)) ? $N - r : d
return d
end
s=0
for r in 1..$N
for c in 1..$N
if distanza(r,c) % 2 == 0
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
| ESERCIZIO 9.D (FOR-IF) |
Costruire un programma che calcoli, nella tavola pitagorica 10x10, la somma dei numeri posizionati:
(Attenzione: non è richiesta la visualizzazione della tabella!)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabella 1 | Tabella 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SOLUZIONE
|
SOLUZIONE
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
$N=10
s=0
for r in 1..$N
for c in 1..$N
cond=(r>=c || (r+c)>=($N+1))
cond=cond && !(r>c && (r+c)>($N+1))
if cond
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
$N=10
s=0
for r in 1..$N
for c in 1..$N
c1=(c+$N/2) % 10 # shift a destra di 5
cond=(r>=c1 || (r+c1)>=($N+1))
cond=cond && !(r>c1 && (r+c1)>($N+1))
if cond
s=s+r*c
print "\u2588\u2588"
else
print "\u2591\u2591"
end
end
print "\n"
end
print "Totale celle azzurre: #{s}" |
| ESERCIZIO 10 (FOR) |
Costruire una breve applicazione che mostra in una tabella 5x5 tutte le possibili coppie (X,Y) ottenibili con le lettere "A", "B", "C", "D" e "E".
Variante: Leggere N caratteri e successivamente generare una tabella NxN con tutte le possibili coppie (X,Y) dei simboli appena acquisiti.
for r in 0..4
for c in 0..4
# Sommo al codice Ascii di "A"
# il progressivo rappresentato da c o r
# in modo da ottenere i simboli successivi
caratt1 = ("A".ord+c).chr
caratt2 = ("A".ord+r).chr
print "("+caratt1+", "+caratt2+") "
end
print "\n"
end
print "Dammi la sequenza: "
s=gets.chomp
n=s.length-1
for r in 0..n
for c in 0..n
caratt1 = s[r]
caratt2 = s[c]
print "("+caratt1+", "+caratt2+") "
end
print "\n"
end
Il doppio ciclo NxN può essere sostituito con un singolo ciclo da 0 a N2-1.
print "Dammi la sequenza: "
s=gets.chomp
n=s.length
for i in 0..(n*n-1)
print "(#{s[i/n]}, #{s[i % n]}) "
if (i % n == (n-1))
print "\n"
end
end
| ESERCIZIO 11 (FOR) |
Costruire una breve applicazione che legge una frase s più tre caratteri a, b e c. Successivamente stampi il numero di occorrenze dei simboli registrati nelle variabili a, b e c all'interno della s.
print "Dammi una stringa: "
s=gets.chomp
print "Dammi 1^ lettera: "
a=gets.chomp
print "Dammi 2^ lettera: "
b=gets.chomp
print "Dammi 3^ lettera: "
c=gets.chomp
nA,nB,nC = 0,0,0
for i in 0..(s.length-1)
nA=nA+1 if s[i]==a
nB=nB+1 if s[i]==b
nC=nC+1 if s[i]==c
end
print "Numero di #{a}=#{nA} - #{b}=#{nB} - #{c}=#{nC}"
| ESERCIZIO 12 (FOR) |
Costruire una breve applicazione che legge un intero n e restituisce la sua scomposizione in fattori primi
# Questo esercizio andrebbe risolto con il WHILE
print "Dammi il numero: "
n=gets.to_i
print "1"
d=2
for i in 2..n
if (n % d == 0)
print "*#{d}"
n=n / d
else
d=d+1
end
end
| ESERCIZIO 13 (FOR) |
Costruire una breve applicazione che legge 2 interi a, b e restituisce minimo comune multiplo e il Massimo Comune Divisore tra a e b
print "Dammi a: "
a=gets.to_i
print "Dammi b: "
b=gets.to_i
minAB=(a < b) ? a : b
maxAB=(a > b) ? a : b
# Minimo comune multiplodivisore
for mcm in maxAB..(a*b)
break if (mcm % a == 0 and mcm % b == 0)
end
# Massimo comune divisore
for mcd in minAB.downto(2)
break if (a % mcd == 0 and b % mcd == 0)
end
print "m.c.m = #{mcm} - M.C.D. = #{mcd}"
| ESERCIZIO 14 (FOR) |
Costruire una breve applicazione che legge un intero n e restituisce l'elenco di tutti i numeri primi minori o uguali di n [un numero è primo se risulta divisibile solo per 1 e per se stesso]
print "Dammi n: "
n=gets.to_i
def ePrimo(n)
for i in 2..(n-1)
if (n % i == 0)
return false
end
end
return true
end
for i in 1..n-1
print "#{i}; " if ePrimo(i)
end
| ESERCIZIO 15 (FOR) |
???
???