3 - STRUTTURE DATI
versione 09/01/2013
I TIPI STRUTTURATI
Una struttura dati è un insieme di tipi diversi di dati raggruppati in un'unica dichiarazione.
I tipi nel corpo della struttura sono chiamati membri della struttura.
La forma della dichiarazione è la seguente:
struct [nome_tipo]
{
tipo1 nome_elemento1;
tipo2 nome_elemento2;
tipo3 nome_elemento3;
.
.
} [nome_variabile];
dove nome_tipo è il nome che assegno alla struttura mentre nome_variabile (opzionale) è un identificatore che denota una variabile
avente nome_tipo come struttura. Tra le parentesi graffe {} sono indicati i tipi e i rispettivi sub_identificatori dei
membri che compongono la struttura. I membri delle strutture possono essere di qualsiasi tipo di dato
e quindi:
- possono contenere altre strutture
- possono contenere puntatori al proprio tipo di struttura (si dicono strutture auto-referenti: utili per
formare strutture dati come liste e alberi).
ma non non possono contenere istanze di se stesse (membri il cui tipo coincide con quello della stessa struttura che sto definendo).
Una volta dichiarata una struttura il suo nome_tipo può essere utilizzato come un nuovo tipo di dati.
La dichiarazione di una struttura non alloca
spazio in memoria ma dichiara solo un tipo nuovo.
Vediamo un esempio:
struct Tipo_Prodotto
{
char nome[30];
float prezzo;
};
Tipo_Prodotto arance, meloni;
Una volta dichiarato, Tipo_Prodotto è diventato un nuovo nome di tipo al pari di quelli fondamentali come int , char o short.
Il campo opzionale nome_variabile che compare alla fine della dichiarazione di una struttura serve a dichiarare direttamente variabili di tale tipo.
Ad esempio avremmo potuto scrivere:
struct Tipo_Prodotto
{
char nome[30];
float prezzo;
} arance, meloni, *frutto;
Se nome_tipo viene omesso non possiamo però dichiarare in seguito altri oggetti dello stesso tipo.
Se non si tratta di una struttura particolare, usata una sola volta all'interno
di un programma, è sempre conveniente definire il nome del tipo di struttura.
Una volta dichiarati i due oggetti arance e meloni possiamo operare sui campi che li costituiscono.
Si accede ai membri di una struttura tramite l’operatore di accesso:
- Se la variabile strutturata è memorizzata sullo stack (memoria statica - ovvero è una variabile dichiarata nel programma stesso)
si usa "." tra il nome della variabile ed il nome del campo.
- Se la variabile strutturata e' memorizzata sullo heap (memoria dinamica - lo spazio è stato allocato con funzioni tipo malloc, calloc
...) si usa "->".
Ad esempio possiamo operare con le seguenti notazioni: arance.nome, arance.prezzo, meloni.nome, meloni.prezzo,
frutto->nome, (*frutto).prezzo.
Attenzione scrivere *frutto.prezzo non è equivalente a (*frutto).prezzo poichè l'operatore
* ha precedenza: quindi *frutto.prezzo corrisponde a *(frutto.prezzo).
// esempio con le strutture
#include <stdio.h>
#include <string.h> // richiesto da strcpy()
struct film_t
{
char titolo [30];
int anno;
} VideoTeca[3], film;
int main ()
{
// INIZIALIZZO
strcpy (VideoTeca[0].titolo, "2001 Odissea nello spazio");
VideoTeca[0].anno = 1968;
strcpy (VideoTeca[1].titolo, "Benvenuti al Nord");
VideoTeca[1].anno = 2011;
// ...
// INPUT
printf("Dammi il titolo: ");
scanf("%s",&film.titolo);
printf("Dammi l'anno: ");
scanf("%d",&film.anno);
VideoTeca[2]=film;
// OUTPUT
printf("1 - %30s => anno: %4d\n",VideoTeca[0].titolo,VideoTeca[0].anno);
printf("2 - %30s => anno: %4d\n",VideoTeca[1].titolo,VideoTeca[1].anno);
printf("3 - %30s => anno: %4d\n",VideoTeca[2].titolo,VideoTeca[2].anno);
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
Le strutture si possono annidare in modo tale che un elemento di una struttura può essere a sua volta una struttura.
Link utili
http://www.math.unipd.it/~sperduti/CORSO-C%2B%2B/Strutture.htm
Il C++ permette di definire nuovi tipi basati su altri tipi di base o precedentemente definiti. Per fare questo si usa la parola chiave
typedef, nel seguente modo:
typedef tipo_esistente nome_nuovo_tipo ;
Vediamone un esempio:
#include <stdio.h>
#include <string.h> // usato da strcpy()
typedef char Carattere;
typedef unsigned int WORD;
typedef Carattere Stringa[30];
typedef struct
{
Stringa nominativo;
WORD eta;
} tPersona;
int main ()
{
tPersona amico;
// INIZIALIZZO
strcpy (amico.nominativo, "Rossi Mario");
amico.eta = 32;
// OUTPUT
printf("%s - anni: %2d\n",amico.nominativo,amico.eta);
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
si osservi:
1) se devo definire un tipo vettoriale la dimensione va posta in fondo alla dichiarazione;
2) L'istruzione typedef può essere inserita anche all'interno di una funzione.
In questo caso la visibilità del tipo predefinito resta accessibile solo quando tale funzione è in
esecuzione
typedef si usa di solito per definire un tipo che viene usato molte volte nel programma e che è possibile debba essere cambiato in una nuova versione del programma. Si usa anche per dare un nome sintetico quando il tipo che si intende utilizzare ha un nome molto complesso.
Le unioni permettono di utilizzare la stessa zona di memoria per memorizzare oggetti appartenenti a tipi differenti. La sua dichiarazione è simile a quella delle strutture ma il suo significato è completamente diverso:
union nome_tipounione
{
tipo1 elemento1;
tipo2 elemento2;
tipo3 elemento3;
.
.
} nome_variabile;
Tutti gli elementi della union occupano lo stesso spazio di memoria. La dimensione di tale spazio è quella dell'elemento che ne richiede di più.
Essi non possono essere valorizzati contemporaneamente in quanto utilizzano la
stessa memoria. Vediamo ora l'esempio:
#include <stdio.h>
int main ()
{
union Mix4Byte_t
{
unsigned long l;
struct
{
unsigned short lo;
unsigned short hi;
} s; // Dichiarazione esplicita
char c[4];
} vMix;
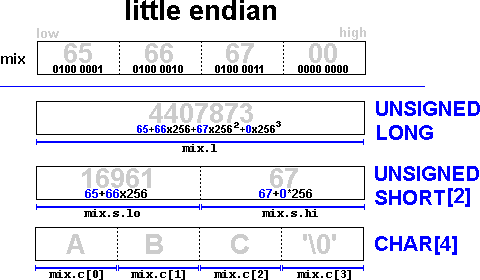
// INIZIALIZZO con:
// (ascii('A')*256^0+ascii('B')*256^1+ascii('C')*256^2+ascii('\0')*256^3
vMix.l = 65 + 66*256 + 67*256*256 + 0*256*256*256;
// OUTPUT
printf("Mostro come unsigned long : l=%lu\n",vMix.l);
printf("Mostro come unsigned short: lo=%u=%hu*256+%hu - hi=%u\n",vMix.s.lo,vMix.c[1],vMix.c[0],vMix.s.hi);
printf("Mostro come char[4] : %s\n",vMix.c);
printf("Mostro come byte[4] : %02hu %02hu %02hu %02hu\n",vMix.c[0],vMix.c[1],vMix.c[2],vMix.c[3]);
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
la cui esecuzione determina questo output:

La particolare inizializzazione segue dal fatto che siamo su architetture Intel e Digital, per cui le informazioni che occupano più byte
sono memorizzate secondo la convenzione little endian ovvero in celle di memoria consecutive dove il byte più significativo si trova nella
cella con indirizzo più alto, mentre quello meno significativo in quella con indirizzo più basso.
In C++ possiamo avere delle unioni anonime. Infatti se inseriamo una unione in una struttura senza indicare il nome di tale
struttura
(il nome che viene di norma posto alla fine, dopo la parentesi graffa) l'unione si dice anonima e possiamo accedere direttamente
agli elementi come fossero campi della struttura. Osserviamo la differenza nelle dichiarazioni del seguente esempio equivalente al precedente:
#include <stdio.h>
int main ()
{
union Mix4Byte_t
{
unsigned long l;
struct
{
unsigned short lo;
unsigned short hi;
}; // Dichiarazione anonima
char c[4];
} vMix;
// INIZIALIZZO con:
// (ascii('A')*256^0+ascii('B')*256^1+ascii('C')*256^2+ascii('\0')*256^3
vMix.l = 65 + 66*256 + 67*256*256 + 0*256*256*256;
// OUTPUT
printf("Mostro come unsigned long : l=%lu\n",vMix.l);
printf("Mostro come unsigned short: lo=%u=%hu*256+%hu - hi=%u\n",vMix.lo,vMix.c[1],vMix.c[0],vMix.hi);
printf("Mostro come char[4] : %s\n",vMix.c);
printf("Mostro come byte[4] : %02hu %02hu %02hu %02hu\n",vMix.c[0],vMix.c[1],vMix.c[2],vMix.c[3]);
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
In realtà era possibile ottenere lo stesso risultato utilizzando una qualsiasi variabile
che occupa 4 byte di memoria (esempio: float, long, char [4]) e poi, utilizzando
opportune tecniche casting, estrarre i valori a seconda del significato desiderato:
#include <stdio.h>
int main ()
{
unsigned long vMix;
// INIZIALIZZO con:
// (ascii('A')*256^0+ascii('B')*256^1+ascii('C')*256^2+ascii('\0')*256^3
vMix = 65 + 66*256 + 67*256*256 + 0*256*256*256;
// OUTPUT
printf("Mostro come unsigned long : l=%lu\n",vMix);
printf("Mostro come unsigned short: lo=%hu - lh=%hu\n",(unsigned short)vMix,*((char *)&vMix+2) );
printf("Mostro come char[4] : %s\n",(char *)&vMix);
printf("Mostro come byte[4] : %02hd %02hd %02hd %02hd\n\n",(char)vMix,*((char *)&vMix+1),*((char *)&vMix+2),*((char *)&vMix+3));
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
Le enumerazioni permettono di creare dei nuovi tipi che non sono basati sui tipi definiti precedentemente. La forma della dichiarazione è la seguente:
enum nome_enum
{
id_valore1,
id_valore2,
id_valore3,
.
.
} [nome_variabile];
Possiamo, ad esempio, creare un nuovo tipo color per memorizzare dei colori. Notiamo che nella dichiarazione
non abbiamo usato nessun tipo di dato fondamentale. Abbiamo creato il nuovo tipo di dato non basato sul tipo colori,
i cui possibili valori sono tutti e soli gli identificatori che abbiamo racchiuso tra parentesi graffe {}:
In realtà il compilatore rappresenta gli elementi di un tipo enumerativo usando degli interi.
Se non specificato altrimenti il primo elemento è rappresentato con 0 ed i successivi con 1,2,... in successione.
Vi è una conversione implicita da tipo enum a int mentre in senso inverso occorre indicare esplicitamente la conversione di tipo.
Ad esempio per calcolare il colore successivo possiamo scrivere C=colori(C+1);
#include <stdio.h>
enum colori
{
verde,
bianco,
rosso
};
int main ()
{
colori C;
C=verde;
printf("Indice: %d\n",C);
C=colori(C+1); // passo al colore successivo
printf("Indice: %d\n",C);
// metto in stop il programma prima della sua chiusura
fflush(stdin);
getchar();
return 0;
}
Link utili
http://www.math.unipd.it/~sperduti/CORSO-C%2B%2B/Tipi%20definiti%20da%20utente.htm
GLI ALGORITMI DI ORDINAMENTO
Un algoritmo di ordinamento è un procedimento che viene utilizzato per elencare gli elementi di un insieme secondo
una sequenza stabilita da una relazione d'ordine, in modo che ogni elemento sia minore (o maggiore) di quello che lo segue.
Un metodo di ordinamento si dice stabile se preserva l'ordine relativo dei dati con chiavi uguali all'interno del file da ordinare.
Ad esempio se si ordina per anno di corso una lista di studenti già ordinata alfabeticamente un metodo stabile produce una lista in
cui gli alunni dello stesso anno sono ancora in ordine alfabetico mentre un ordinamento instabile probabilmente produrrà una lista
senza più alcuna traccia del precedente ordinamento.
Un algoritmo si dice algoritmo in place quando non crea una copia dell'input per raggiungere l'obiettivo, l'ordinamento in questo caso.
Pertanto un algoritmo in place risparmia memoria.
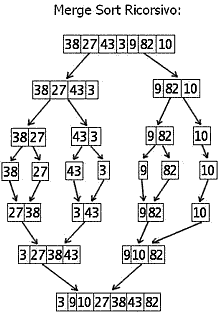
MERGE SORT
Il merge sort è un algoritmo di ordinamento molto intuitivo e abbastanza rapido, che utilizza un processo di risoluzione ricorsivo.
L'idea alla base del merge sort è il procedimento Divide et Impera, che consiste nella suddivisione del problema in sottoproblemi via via più piccoli.
Il merge sort opera quindi dividendo l'insieme da ordinare in due metà e procedendo all'ordinamento delle medesime ricorsivamente.
Quando si sono divise tutte le metà si procede alla loro fusione (merge appunto) costruendo un insieme ordinato. L'algoritmo fu inventato da
John von Neumann nel 1945. In dettaglio l'algoritmo funziona in questo
modo:
- Se la sequenza da ordinare ha lunghezza 0 oppure 1, è già ordinata.
- La sequenza viene divisa (divide) in due metà (se la sequenza contiene un numero dispari di elementi, viene divisa in due sottosequenze
di cui la prima ha un elemento in più della seconda)
- Ognuna di queste sottosequenze viene ordinata, applicando ricorsivamente l'algoritmo(impera)
- Le due sottosequenze ordinate vengono fuse (combina) e ordinate. Per fare questo, si estrae ripetutamente il minimo delle due sottosequenze e lo si pone nella sequenza in uscita,
che risulterà ordinata
L'algoritmo può essere implementato fondamentalmente tramite due tecniche:
- Top-Down (ricorsiva): che è quella presentata nell'esempio precedente: opera su un insieme e lo divide in sotto insiemi fino ad arrivare all'insieme contenente un solo elemento,
per poi riunire ordinando le parti scomposte;
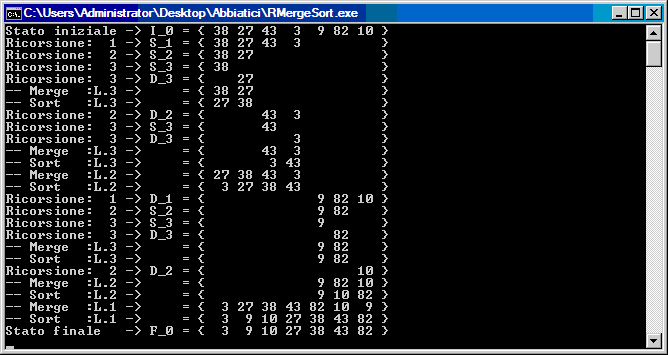
#include <stdio.h>
const int n=7;
int v[]={38, 27, 43, 3, 9, 82, 10};
void StampaVettoreMerge(int v[], int da , int a, char p[],int livello)
{
printf("%s :L.%d -> = { ",p,livello);
for (int k=0; k < da ; printf(" "), k++);
for (int k=da; k <= a ; printf("%2d ", v[k]), k++);
for (int k=a+1; k < n ; printf(" "), k++);
printf("}\n");
}
void StampaVettore(int v[], int da , int a, int iteraz, char dove)
{
if (dove=='I')
printf("Stato iniziale -> %c_0 = { ",dove);
else if (dove=='F')
printf("Stato finale -> %c_0 = { ",dove);
else
printf("Ricorsione:%3d -> %c_%d = { ",iteraz,dove,iteraz);
for (int k=0; k < da ; printf(" "), k++);
for (int k=da; k <= a ; printf("%2d ", v[k]), k++);
for (int k=a+1; k < n ; printf(" "), k++);
printf("}\n");
}
void merge(int a[], int left, int center, int right, int livello)
{
int* aux = new int[right + 1];
int i,j;
// UNISCO I DUE SOTTO VETTORI
for (i = center+1; i > left; i--)
aux[i-1] = a[i-1];
for (j = center; j < right; j++)
aux[right+center-j] = a[j+1];
StampaVettoreMerge(aux,left,right,"-- Merge",livello);
// ORDINO I DUE SOTTO VETTORI
for (int k = left; k <= right; k++)
if (aux[j] < aux[i])
a[k] = aux[j--];
else
a[k] = aux[i++];
StampaVettoreMerge(a,left,right,"-- Sort ",livello);
delete aux;
}
void mergesort(int a[], int left, int right, int livello, char dove)
{
StampaVettore(a,left,right,livello,dove);
if (left < right)
{
int center = (left+right)/2;
mergesort(a, left, center, livello+1,'S');
mergesort(a, center+1, right,livello+1,'D');
merge(a, left, center, right, livello+1);
}
}
int main()
{
//int v[n] = {10, 3, 15, 2, 1, 4, 9, 0};
mergesort(v,0,n-1,0,'I');
StampaVettore(v,0,n-1,0,'F');
fflush(stdin);
getchar();
return 0;
}
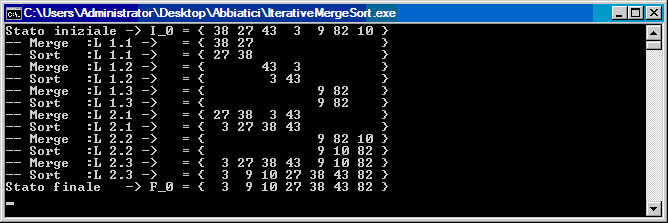
- Bottom-Up (iterativa): che consiste nel considerare l'insieme come composto da un vettore di sequenze. Ad ogni passo vengono fuse due sequenze.
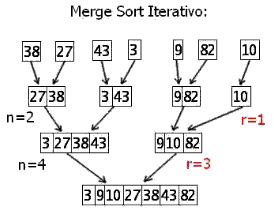
Ecco la versione iterativa:
#include <stdio.h>
const int n=7;
int v[]={38, 27, 43, 3, 9, 82, 10};
void StampaVettore(int v[], int da , int a, int iteraz, char dove)
{
if (dove=='I')
printf("Stato iniziale -> %c_0 = { ",dove);
else if (dove=='F')
printf("Stato finale -> %c_0 = { ",dove);
else
printf("Iterazione:%3d -> %c_%d = { ",iteraz,dove,iteraz);
for (int k=0; k < da ; printf(" "), k++);
for (int k=da; k <= a ; printf("%2d ", v[k]), k++);
for (int k=a+1; k < n ; printf(" "), k++);
printf("}\n");
}
void StampaVettoreMerge(int v[], int da , int a, char p[],int livello, int step)
{
printf("%s :L %d.%d -> = { ",p,livello,step);
for (int k=0; k < da ; printf(" "), k++);
for (int k=da; k <= a ; printf("%2d ", v[k]), k++);
for (int k=a+1; k < n ; printf(" "), k++);
printf("}\n");
}
void merge(int a[], int start, int center, int end, int size, int livello, int step)
{
int i, j, k;
int app[size];
// i punta agli elementi a sinistra - j a quelli a destra
// confronta due elementi dei 2 sottovettori e estrae il + piccolo
// che copia nell'array di supporto
for (k=0, i=start, j=center+1 ; (i<=center) && (j<=end); k++ )
if (a[i] <= a[j])
app[k] = a[i++];
else
app[k] = a[j++];
while (i<=center)
app[k++] = a[i++];
while (j<=end)
app[k++] = a[j++];
StampaVettoreMerge(a,start,end,"-- Merge",livello,step);
for (k=start; k<=end; k++)
a[k] = app[k-start];
StampaVettoreMerge(a,start,end,"-- Sort ",livello,step);
}
void Iterative_Mergesort(int a[],int size)
{
int sizetomerge=size-1;
size--;
int i,j;
int m=2; // ampiezza intervallo analizzato
int livello=0;
StampaVettore(v,0,sizetomerge,livello,'I');
while (m < sizetomerge*2)
{
livello++;
// Analizzo le sottosequenze lunghe m
for (i=0,j=1; (i+m-1) <= sizetomerge; i+=m)
merge(a,i,(2*i+m-1)/2,i+(m-1),sizetomerge,livello,j++);
i--;
if ( (sizetomerge+1)%m!=0)
{
if (size > sizetomerge)
merge (a,sizetomerge -((sizetomerge)%m),sizetomerge,size,size,livello,j++);
sizetomerge=sizetomerge-((sizetomerge+1)%m);
}
m=m*2;
}
if (size > sizetomerge)
merge (a,0,size-(size-sizetomerge),size,size,livello,j++);
}
int main()
{
Iterative_Mergesort(v,n);
StampaVettore(v,0,n-1,0,'F');
fflush(stdin);
getchar();
return(0);
}
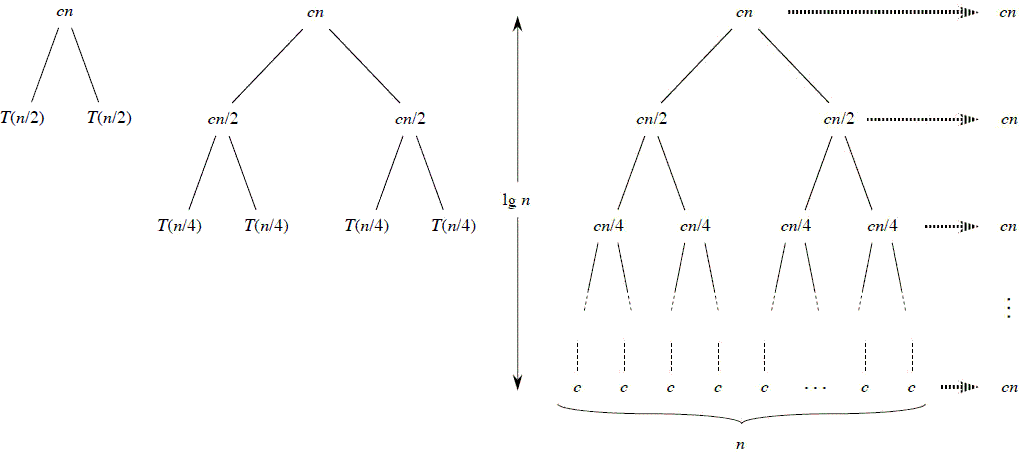
L'algoritmo Merge Sort, per ordinare una sequenza di oggetti, ha complessità temporale, sia nel caso medio che nel caso pessimo pari a: T(n)=Θ(n*log2n).
come si può facilmente intuire dalla figura sottostante dove cn è il costo è la funzione di costo della fase di suddivisione del problema e di ricostruzione della soluzione (sarebbe meglio usare f(n))
INSERTION SORT
L'insertion sort è un algoritmo relativamente semplice per ordinare un array.
Caratteristiche salienti:
-
Non è molto diverso dal modo in cui un essere umano, spesso, ordina un mazzo di carte.
-
E' un algoritmo in place, cioè ordina l'array senza doverne creare una copia, risparmiando memoria.
-
Pur essendo molto meno efficiente di algoritmi più avanzati, può avere alcuni vantaggi: ad esempio:
-
La sua evoluzione è rappresentata dallo "Shell Sort".
Vediamo come è possibile ordinare il nostro elenco X={X0, X1, ... , Xn-1}.
Per semplicità consideriamo un elenco di numeri non ordinato. Procediamo nel modo seguente:
Inizializzazione:
- dividiamo la sequenza X in due sottosequenze Sk={X0, ... Xk} e
Dk={Xk+1, ... Xn-1}.
Immaginiamo che la sottosequenza a sinistra Sk sia
ordinata (questa ipotesi è vera visto che la sottosequenza iniziale S0
è composta da un solo
elemento: { X0}).
Per l'altra sequenza D0 non possiamo ipotizzare nulla relativamente all'ordinamento.
Step k=0
- Iniziamo considerando k=0. Nel caso la sequenza sia composta dai
valori sottostanti S0
è D0 risultano:
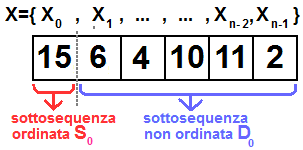
- Confrontiamo l'ultimo ed unico elemento
X0 di
S0 con il primo X1 della sequenza D0.
- Se X0 è minore o uguale di X1 non faccio niente
(Xk <= Xk+1)
- Se invece invece X0 è maggiore di X1
(Xk > Xk+1) allora
lo scambio di posto con X1. Per effettuare questo scambio occorre utilizzare una variabile di supporto
t dove memorizzo temporaneamente il valore X1 da spostare.
- Con questo spostamento mi
ritrovo una sequenza S1 (Sk+1) che risulta ordinata e che ha un elemento in più
(preso dal Dk originale) rispetto all' S0 iniziale.

Step k-esimo
- Generalizziamo per la k-esima iterazione. Ipotizziamo che
l'esecuzione dei precedenti passaggi ci abbia permesso di ottenere una
sottosequenza ordinata Sk
contenente k+1 elementi. Preleviamo quindi il primo elemento Xk+1 della sequenza Dk (in
realtà la scelta può essere del tutto arbitraria) e lo memorizziamo in
una variabile di supporto t.
.
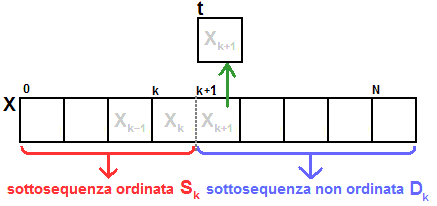
- Uno ad uno facciamo slittare di un posto verso destra, partendo dagli ultimi
elementi della sottosequenza ordinata Sk, tutti gli elementi
Xi fino a ché
risulta vera la relazione Xi > t con i
che decresce da k fino a 0.
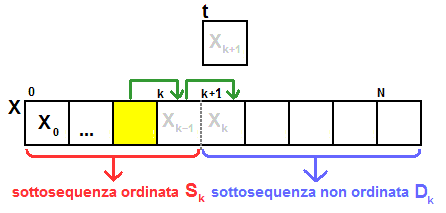
- Nella cella liberata viene inserito il contenuto della variabile t
(contiene Xk+1) che risulta essere ancora maggiore o uguale dell'elemento alla sua sinistra e minore
dell'elemento alla sua destra
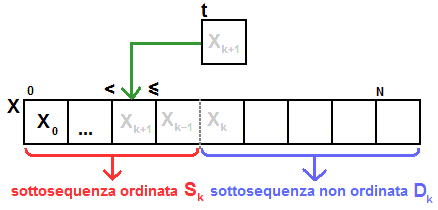
- Avendo inserito l'elemento t
(contiene Xk+1) nella posizione corretta ottengo una nuova sottosequenza ordinata Sk+1 risulta estesa di un ulteriore elemento.
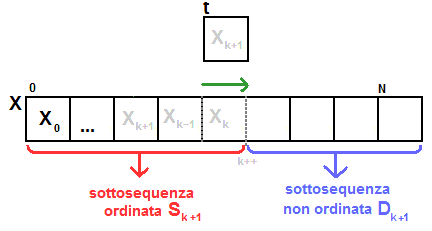
- ripeto i passaggi fino a che k diventa pari a n e quindi Dk diventa l'insieme vuoto.
Sk alla fine conterrà tutti gli elementi della sequenza originale X disposti in modo ordinato.
Per implementare questo algoritmo occorrono due indici:
- uno punta all'elemento separatore tra i due insiemi Sk e Dk.
- il secondo è usato per scorrere gli elementi di Sk che
devono essere spostati verso destra.
L'algoritmo così tende a spostare man mano gli elementi maggiori verso destra.
#include <stdio.h>
#define N 8
void StampaVettore(int v[], int n, int iteraz)
{
if (iteraz==0)
printf("Stato iniziale -> S_0 = {");
else
printf("Iterazione:%3d -> S_%d = {",iteraz,iteraz);
for (int k=0; k < n ; printf("%2d %s", v[k], (k==iteraz) ? "} - {" : "" ), k++);
printf("}\n");
}
void InsertionSort( int X[], int n )
{
int k, p, t;
StampaVettore(X,n,0);
for (k = 0; k < n-1 ; k++) // Gestisce S_k e D_k
{
t=X[k+1]; // primo di D_k
for ( p=k ; p >= 0 && X[p] > t ; p--)
X[p+1]=X[p];
X[p+1]=t; // metto X_(k+1) nello spazio che ho liberato
StampaVettore(X,n,k+1);
}
}
int main()
{
int X[8]={ 3, 7, 4, 9, 5, 2, 6, 1 };
printf("INSERTION SORT\n");
InsertionSort(X,N);
//InsertionSort_Saetti(X,N);
fflush(stdin);
getchar();
return(0);
}
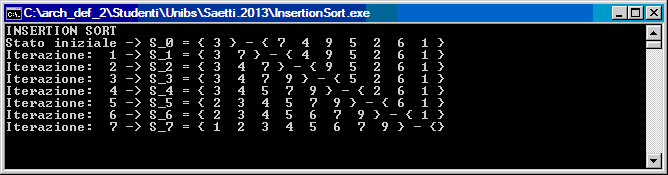
Per quanto riguarda il numero di confronti e spostamenti il caso ottimo per
questo l'algoritmo è quello in cui la sequenza di partenza è già ordinata. In questo caso, l'algoritmo ha tempo di esecuzione lineare, ossia
O(n). Infatti, in questo caso, in ogni iterazione il primo elemento della sottosequenza non ordinata viene confrontato solo con l'ultimo della sottosequenza ordinata. Il
caso pessimo è invece
rappresentato da una sequenza di partenza ordinata in modo inverso. In questo caso, ogni iterazione dovrà scorrere e spostare ogni elemento della sottosequenza ordinata prima di poter inserire il primo elemento della sottosequenza non ordinata. Pertanto, in questo caso l'algoritmo di
insertion sort ha complessità temporale quadratica, ossia O(n2).
Anche il caso medio ha complessità quadratica, il che lo rende impraticabile per ordinare sequenze grandi. Pur avendo complessità elevata, tuttavia, risulta essere l'algoritmo di ordinamento più veloce per array piccoli.
L'algoritmo di "Insertion Sort" che ha un tempo di esecuzione Θ(n2) (caso peggiore) risulta + lento del Merge Sort.
SELECTION SORT
Il selection sort è un algoritmo di ordinamento che opera
in place ed in modo molto simile all'ordinamento per inserzione
(insertion sort). Mentre nell'insertion
sort l'elemento scelto in Dk per lo swap con
l'ultimo elemento Xk di Sk
è quello in prima posizione (ovvero Xk+1)
nel selection sort è quello che in
Dk assume il valore minimo
Xkmin.
L'algoritmo è di tipo non adattivo,
ossia il suo tempo di esecuzione non dipende dall'input ma dalla dimensione
dell'array.
Vediamo come è possibile ordinare il nostro elenco X={X0, X1, ... , Xn-1}.
Procediamo nel modo seguente:
Inizializzazione:
La sequenza X
viene suddivisa in due parti Sk e Dk
con k da 0 a n-1:
- Sk={X0, ... Xk}
la sottosequenza che occupa le prime posizioni dell'array,
- la
sottosequenza Dk={Xk+1, ... Xn-1}
che costituisce la parte restante dell'array.
Immaginiamo che la
sottosequenza a sinistra Sk sia
ordinata (questa ipotesi è vera sicuramente all'inizio visto che la
sottosequenza di partenza S0
è composta da un solo elemento { X0 }).
Per l'altra sequenza D0 non ipotizziamo nulla relativamente all'ordinamento.
Step k=0
Iniziamo considerando k=0. L'algoritmo seleziona l'elemento minore
Xkmin nella sequenza
D0 e se questo risulta inferiore con l'unico elemento X0
di S0 lo sposta, mediante uno scambio con X0, nella
sottosequenza ordinata S0.
Step k-esimo
Generalizziamo: dovendo ordinare un array X di lunghezza n, si
fa scorrere l'indice k da 1 a n-1 ripetendo i
seguenti passi:
-
si cerca il più piccolo elemento
Xkmin della sottosequenza Dk={Xk+1, ... Xn-1};
-
se
Xkmin risulta minore
dell'ultimo elemento Xk
di Sk lo si scambia con l'elemento Xk
di Sk.
La complessità di tale algoritmo è dell'ordine di θ(n2).
Infatti il ciclo interno è un semplice test per confrontare l'elemento
corrente con l'elemento minimo trovato fino a quel momento (più il codice per
incrementare l'indice dell'elemento corrente e per verificare che esso non
ecceda i limiti dell'array). Lo spostamento degli elementi è fuori dal
ciclo interno: ogni scambio pone un elemento nella sua posizione finale quindi
il numero massimo di scambi è pari a N-1 (dato che l'ultimo elemento non deve
essere scambiato).
Un inconveniente dell'algoritmo di ordinamento per selezione è
che il tempo di esecuzione dipende solo in modo modesto dal grado di ordinamento
in cui si trova il file. La ricerca del minimo elemento durante una scansione
del file non sembra dare informazioni circa la posizione del prossimo minimo
nella scansione successiva. Chi utilizza questo algoritmo potrebbe stupirsi nel
verificare che esso impiega più o meno lo stesso tempo sia su file già ordinati
che su file con tutte le chiavi uguali, o anche su file ordinati in modo
casuale.
L'ordinamento per
selezione ha un'importante applicazione: poiché ciascun elemento viene spostato
al più una volta, questo tipo di ordinamento è il metodo da preferire quando si
devono ordinare file costituiti da record estremamente grandi e da chiavi molto
piccole. Per queste applicazioni il costo dello spostamento dei dati è
prevalente sul costo dei confronti e nessun algoritmo è in grado di ordinare un
file con spostamenti di dati sostanzialmente inferiori a quelli dell'ordinamento
per selezione.
Ecco il programma sorgente
#include <stdio.h>
#define N 8
void StampaVettore(int v[], int n, int iteraz)
{
if (iteraz==0)
printf("Stato iniziale -> S_0 = {");
else
printf("Iterazione:%3d -> S_%d = {",iteraz,iteraz);
for (int k=0; k < n ; printf("%2d %s", v[k], (k==iteraz) ? "} - {" : "" ), k++);
printf("}\n");
}
void SelectionSort( int X[], int n )
{
int k, h, posmin, t;
for (k = 0; k <= n-2 ; k++) // k gestisce S_k e D_k
{
StampaVettore(X,n,k);
posmin=k; // prendo come minimo iniziale l'ultimo elemento X_k di S_k
for (h = k+1; h < n ; h++) // Ricerco il minimo nel'insieme D_k
if (X[h] < X[posmin])
posmin=h;
if (posmin!=k) // se il minimo di D_k è minore di X_k effettuo lo swap
{
t=X[k];
X[k]=X[posmin];
X[posmin]=t;
}
}
StampaVettore(X,n,k);
}
int main()
{
int X[8]={ 3, 7, 4, 9, 5, 2, 6, 1 };
printf("SELECTION SORT\n");
SelectionSort(X,N);
fflush(stdin);
getchar();
return(0);
}
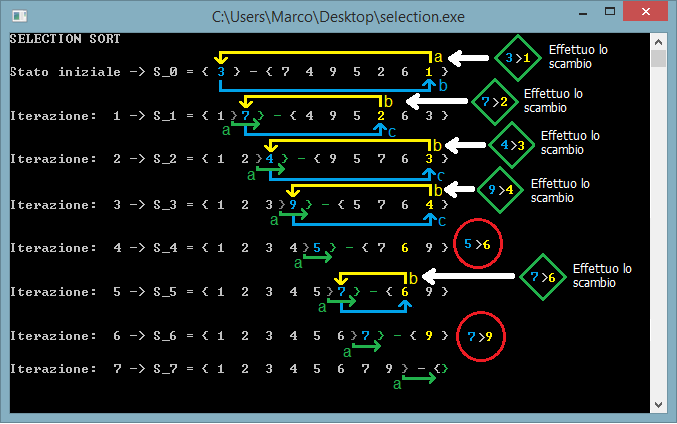
Come si nota dall'esecuzione il minimo
Xkmin della sequenza Dk
viene confrontato con l'ultimo elemento Xk
di Sk e se
Xkmin risulta
minore di Xk allora
viene fatto lo swap tra i 2 elementi.
BUBBLE SORT
Il Bubble sort è un semplice algoritmo di ordinamento di
dati. Il suo funzionamento è semplice: ogni coppia di elementi adiacenti della
lista viene comparata e se sono nell'ordine sbagliato vengono invertiti di
posizione. L'algoritmo continua a ripetere lo scorrimento di tutta la lista
finché non vengono più eseguiti scambi, situazione che indica che la lista è
ordinata.
Il Bubble sort non è un algoritmo
efficiente: ha una complessità computazionale dell'ordine di θ(n2)
confronti, con n elementi da ordinare; si usa solamente a scopo
didattico in virtù della sua semplicità, e per introdurre i futuri programmatori
al ragionamento algoritmico e alle misure di complessità.
Il
bubble sort è un algoritmo iterativo, basato sulla ripetizione
di un procedimento fondamentale. La singola iterazione dell'algoritmo prevede
che gli elementi dell'array siano confrontati a due a due, procedendo in un
verso stabilito.
Per esempio ad ogni ciclo iterativo verranno
confrontati:
- il primo e il secondo elemento - se non sono
ordinati verranno scambiati di posizione,
- il secondo e il terzo - se non sono ordinati verranno scambiati
di posizione,
- il terzo e il quarto - se non sono ordinati
verranno scambiati di posizione,
- .. e così via ...
- il penultimo e
l'ultimo elemento - se non sono ordinati verranno scambiati di posizione.
Durante ogni ciclo iterativo almeno un valore viene spostato fino
a raggiungere la sua collocazione definitiva; in particolare, alla prima
iterazione il numero più grande raggiunge l'ultima posizione dell'array, alla
seconda il secondo numero più grande raggiunge la penultima posizione, e così
via. Quindi dopo la prima iterazione l'elemento più grande si troverà certamente
nell'ultima posizione della lista: quella sua definitiva; alla seconda
iterazione il secondo più grande si troverà in penultima posizione, quella sua
definitiva, e così via
Ecco il codice sorgente
#include <stdio.h>
#include
#define N 8
void StampaVettore(int v[], int n, int iteraz, int nswap)
{
if (nswap==-1)
{
if (iteraz==0)
printf("Stato iniziale ----> {");
else
printf("Iterazione:%3d ----> {",iteraz,iteraz);
}
else
printf(" swap X[%d]<->X[%d] {",nswap,nswap+1);
for (int k=0; k < n ; printf("%2d ", v[k]), k++);
printf("}\n");
if (iteraz==0 || nswap==-1) return;
printf(" ");
for (int k=0; k < nswap ; printf(" "), k++);
printf(" <-->\n");
}
void BubbleSort( int X[], int n )
{
bool HoScambiato;
int k=0, i, t;
StampaVettore(X,n,k++,-1); // non necessario
do
{
StampaVettore(X,n,k++,-1); // non necessario
HoScambiato = false;
for (i = 0; i <= n-2 ; i++)
{
if (X[i] > X[i+1]) // Swap
{
t=X[i];
X[i]=X[i+1];
X[i+1]=t;
HoScambiato =true;
StampaVettore(X,n,k,i); // non necessario
}
}
}
while (HoScambiato); // finchè effettuo Swap ripercorro l'array partendo dall'inizio
}
int main()
{
int X[8]={ 3, 7, 4, 9, 5, 2, 6, 1 };
printf("BUBBLE SORT\n");
BubbleSort(X,N);
fflush(stdin);
getchar();
return(0);
}
Ecco cosa viene mostrato durante l'esecuzione di tale codice

Ottimizzazioni
Le
prestazioni del bubble sort possono essere leggermente migliorate tenendo conto
del fatto che dopo la prima iterazione l'elemento più grande si troverà
certamente nell'ultima posizione della lista, quella sua definitiva; alla
seconda iterazione il secondo più grande si troverà in penultima posizione,
quella sua definitiva, e così via. Ad ogni iterazione il ciclo dei confronti può
accorciarsi di un passo rispetto al precedente evitando di scorrere ogni volta
tutta la lista fino in fondo: all'n-esima iterazione si può quindi fare a meno
di trattare gli ultimi n-1 elementi che ormai si trovano nella loro posizione
definitiva. Possiamo rappresentare quanto detto con questo secondo pseudocodice:
void BubbleSort( int X[], int n )
{
bool HoScambiato;
int k=0, i, t;
int fine=n-2;
StampaVettore(X,n,k++,-1); // non necessario
do
{
StampaVettore(X,n,k++,-1); // non necessario
HoScambiato = false;
for (i = 0; i <= fine ; i++)
{
if (X[i] > X[i+1]) // Swap
{
t=X[i];
X[i]=X[i+1];
X[i+1]=t;
HoScambiato =true;
StampaVettore(X,n,k,i); // non necessario
}
}
fine--;
}
while (HoScambiato); // finchè effettuo Swap ripercorro l'array partendo dall'inizio
}
Un altro tipo di ottimizzazione deriva dall'osservazione che spesso, alla fine
di una iterazione, non uno bensì due o più elementi si trovano nella loro
posizione definitiva. In realtà tutti gli elementi che si trovano a valle
dell'ultimo scambio effettuato risultano ordinati e si può evitare di trattarli
ancora nell'iterazione successiva.
Possiamo rappresentare quanto detto
con questo terzo pseudocodice:
void BubbleSort( int X[], int n )
{
int k=0, i, t, UltimoScambiato;
int fine=n-2;
StampaVettore(X,n,k++,-1); // non necessario
do
{
StampaVettore(X,n,k++,-1); // non necessario
UltimoScambiato=0;
for (i = 0; i <= fine ; i++)
{
if (X[i] > X[i+1]) // Swap
{
t=X[i];
X[i]=X[i+1];
X[i+1]=t;
UltimoScambiato=i;
StampaVettore(X,n,k,i); // non necessario
}
}
fine=UltimoScambiato;
}
while (UltimoScambiato>0); // finchè effettuo Swap ripercorro l'array partendo dall'inizio
}
QUICK SORT
Il Quick sort è un
Link utili
http://www.math.unipd.it/~sperduti/CORSO-C%2B%2B/Tipi%20definiti%20da%20utente.htm















