Le soluzioni vanno pubblicate seguendo le direttive del docente.
Se è richiesta la pubblicazione nel Registro del Professore online allora occorre creare un unico file ODS/XLS. Tutte le soluzioni proposte devono rispettare questi vincoli:
1) Le formule devono essere scritte nelle celle con tonalità
grigie o
azzurra. Le
grigie vanno intese come celle di supporto
ai calcoli mentre quelle azzurre
come celle di output.
3) Le celle gialle rappresentano le
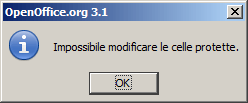
uniche celle di input e devono essere le sole modificabili. In altre
parole se cerco di scrivere su una qualsiasi altra cella (non gialla) si deve visualizzare questo
messaggio di errore.

3) L'aspetto grafico deve essere identico alle immagini
riportate nell'esercitazione
4) Il file uploadato deve presentare più fogli come indicato nella figura
sottostante.
![]()
5) Le colonne e le righe non visibili
nelle immagini devono essere nascoste.
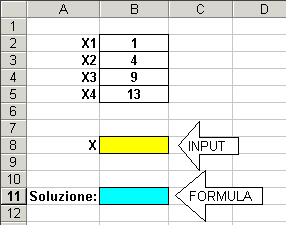
6) Le frecce "INPUT" e "FORMULA" presenti nelle figure non vanno
inserite.
Ogni studente deve pubblicare la propria
soluzione anche se sviluppata in collaborazione con altri compagni. Le varianti sono richieste ad esclusione di
quelle indicate come facoltative. Uploadare le vostre soluzioni seguendo le
scadenze indicate nel forum o dal docente. Il nome del file contenente il vostro
lavoro deve essere:
- ESER_AV.ZIP
per gli esercizi base
- ESER_AVVAR.XLS per quelli con le varianti obbligatorie
- ESER_AVFACO.XLS per quelli con le varianti facoltative.
L'esercizio 0 è un esempio e non deve essere aggiunto alle vostre soluzioni
| ESERCIZIO DI ESEMPIO |
Si consideri un intervallo sull'asse X
delimitato dai punti indicati nelle celle C2 e C3.
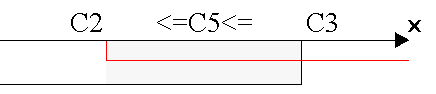

Si scriva in C8 la formula (usando una solo
funzione SE!) che visualizza la frase "C5 appartiene
all'intervallo [C2,C3]" quando il punto indicato in C5
è interno all'intervallo mentre visualizza la frase "C5 non appartiene
all'intervallo [C2,C3]" altrimenti. Naturalmente al posto
degli indirizzi delle celle si dovrà vedere il valore contenuto nelle celle.
PS: per unire delle parole in Excel si
deve utilizzare l'operatore di concatenazione tra stringhe &. Esempio
"Mario " & "Rossi" ==> "Mario Rossi"
SOLUZIONE
Formula nella cella A7:
=SE(E(C5<=C3;C5>=C2);C5 & " appartiene a [" & C2 &"-" & C3 &"]";C5 & " non
appartiene[" & C2 &"-" & C3 &"]")
| ESERCIZIO M1.2.1 |
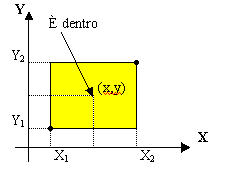
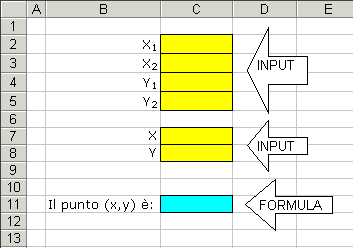
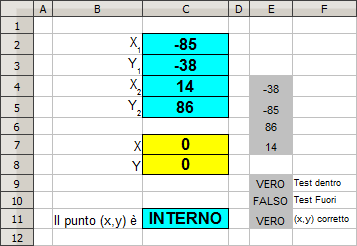
Costruire in C11 la formula che indichi se il
punto (C7,C8) [X,Y] è, rispetto al rettangolo con angolo inferiore sinistro
(C2,C4) [X1,Y1] e angolo superiore destro (C3,C5)
[X2,Y2],:
- "interno"
- "esterno"
- "sul bordo"
Attenzione: le formule utilizzate non devono contenere riferimenti espliciti alle celle
(esempio B2 o $C$3) [suggerimento: definire per le celle dei nomi: X_1, X_2, ...]. E'
consentito l'uso di celle di supporto.
VARIANTE: Aggiungere
all'esercizio le seguenti funzionalità:
- la generazione automatica delle coordinate (X1,Y1)
[angolo inferiore sinistro] e (X2,Y2) [angolo superiore
destro] relative al rettangolo. I punti generati devono stare dentro il quadrato
(-100;-100) e (100,100).
- il controllo dell'input per le coordinate (X,Y). Ad esempio se X
o Y risultano errati allora la cella C11 deve restare vuota
Suggerimento: utilizzare le funzioni:
PICCOLO(Area;Posizione)
e
CASUALE()
(questa funzione è presente anche in OOCalc)
Ricordo che l'espressione
=CASUALE()*(B-A)+A
consente di generare un numero
nell'intervallo
[A,B)
In OOCALC
si può utilizzare anche la funzione:
CASUALE.TRA(A;B)
che genera
un numero nell'intervallo [A,B) (ma non si aggiorna con il tasto di ricalcola
F9)
| ESERCIZIO M1.2.2 |
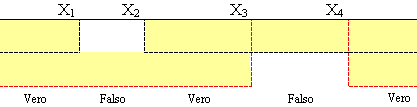
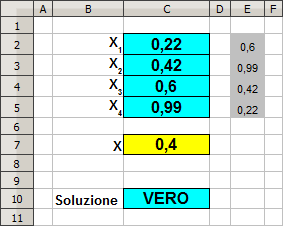
Si scriva in B11 la funzione che restituisce "FALSO" quando il valore in B8 è compreso tra B2 e B3 oppure tra B4 e B5, VERO altrimenti
VARIANTE: Aggiungere
all'esercizio le seguenti funzionalità:
- la generazione automatica delle coordinate (X1,X2,X3,X4).
I punti generati devono stare dentro l'intervallo [0,1)
- il controllo dell'input nella cella C7. Ad esempio se non è stata digitata correttamente la X
in B11 deve apparire la scritta "???".
Suggerimento: utilizzare le funzioni:
CASUALE()
e
PICCOLO(Area;Posizione)
| ESERCIZIO M1.2.3 |
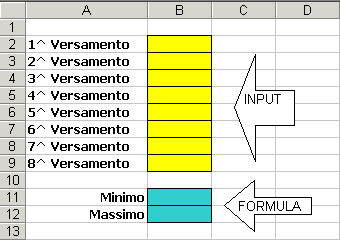
Si considerino 8 versamenti (durante l'interrogazione il
numero di versamenti può essere anche di 30 movimenti!). Fornire una soluzione,
basata unicamente sulla funzione SE(...;...;...)
che restituisca in B11 e B12 il versamento Minimo e Massimo. I
valori devono essere visualizzati con il separatore delle migliaia e con al
massimo due cifre decimali. Deve apparire anche il segno della valuta dell'euro: €.
Non
è ammesso quindi l'uso di nessun altra funzione come:
PICCOLO(),
GRANDE(),
MIN(),
MAX()
etc.
E' possibile utilizzare delle colonne di supporto. Non è richiesto alcun
controllo dell'input. La soluzione proposta deve essere applicabile anche a
100.000 versamenti.
VARIANTE: fornire:
- 3 soluzioni: la prima deve utilizzare la coppia di funzioni
MIN()e
MAX();
la seconda
solo la funzione
PICCOLO()
mentre la terza solo la funzione
GRANDE().
- visualizzare la stringa "????" qualora almeno uno dei
versamenti sia vuoto o errato (ad esempio contiene lettere). Non è ammesso l'uso di celle di supporto. Ulteriori funzioni
utilizzabili sono:
SE,
CONTA.NUMERI
e
CONTA.SE.
| ESERCIZIO M1.2.4 |

Si considerino 8 possibili movimenti bancari. Costruire
(utilizzando solo
SOMMA.SE) un meccanismo capace di restituire la
differenza tra i versamenti e i prelievi (saldo). Gli importi devono essere
visualizzati con al massimo due cifre decimali. Non è richiesto alcun controllo
dell'input.
VARIANTE: (richiesta a partire dall'A.S. 2012-2013) fornire
una soluzione che utilizza solo le funzioni
SOMMA
e
SE.
E' ammesso l'uso di celle di supporto.
| ESERCIZIO M1.2.5 |
Si consideri un elenco di 10 persone (durante l'interrogazione il numero potrebbe essere superiore a 30!) come nella figura
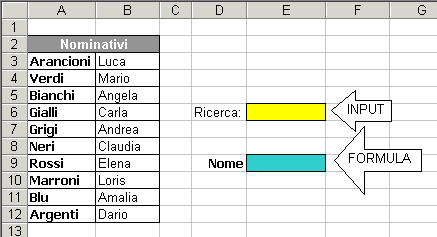
Scrivere in E9 la formula che restituisce la parola "ASSENTE" se il cognome inserito in E6 non è in elenco altrimenti mostra il nome della persona cercata. E' ammesso l'uso solo di funzioni come MAIUSC (in OOCalc), E, O, SE. Quindi non è possibile usare altre funzioni come ad esempio: CERCA.VERT. Quando la cella E6 è vuota in E9 non deve essere visualizzato niente. La soluzione proposta non deve essere case sensitive (non distingue tra maiuscolo e minuscolo!).
VARIANTE: Lo stesso esercizio ma questa volta
utilizzando la funzione
CERCA.VERT. L'errore
#N/D (che appare quando non viene trovato il cognome) deve essere gestito
sostituendolo con la parola ASSENTE. Suggerimento: controllate la sintassi della
funzione
VAL.ERRORE.
Quando la cella E6 è vuota anche E9
non deve visualizzare niente.
| ESERCIZIO M1.2.6 (facoltativo) |

Ampliare l'esercizio del Master Mind, proposto nella precedente
esercitazione, in modo che oltre al numero di colori in posizione corretta venga
restituito il numero dei colori indovinati ma con posizione errata. Vanno
quindi esclusi da questo conteggio quelli già
posizionati correttamente. Attenzione i colori possono essere ripetuti!
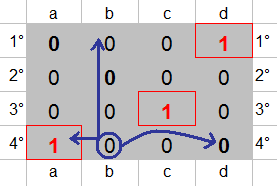
Suggerimento: utilizzare delle celle di supporto disposte in un'area 4x4.
Nella generica cella (i,j) metteremo 1 quando valgono queste condizioni:
- Tiro(i)=Codice(j) (i=a,b,c,d - j=1°,2°,3°,4°)
- Se gli elementi sulla riga j e colonna i, per le quali vale la
relazione Tiro(i)=Codice(j), non hanno
mai determinato un valore 1
| ESERCIZIO M1.2.7 |
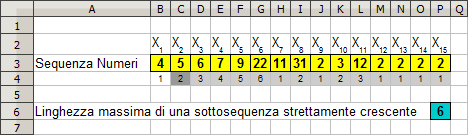
Una sequenza di numeri si dice strettamente crescente
quando ogni termine Xn risulta maggiore del suo precedente Xn-1.
Si consideri quindi una sequenza di 15 numeri digitati dall'utente. Costruire
una soluzione che restituisca in P6 la lunghezza massima raggiunta da una
sottosequenza strettamente crescente contenuta nei 15 numeri digitati
Nella soluzione, le formule di supporto scritte nelle
celle grigio chiaro devono essere
inserite mediante un'operazione di copia ed incolla partendo dalle celle
grigio scuro.
| ESERCIZIO M1.2.8 |
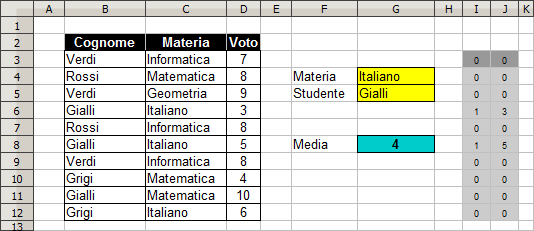
Si consideri l'elenco di tutte le interrogazioni orali,
distinte per materia, degli studenti di una determinata classe. Costruire la soluzione che
calcola in G8 il voto medio dello studente (vedi cella G5) nella
materia (vedi cella G4). Nella cella G8 la vostra soluzione
dovrà visualizzare:
- niente: se non è stata digitata la materia o lo studente
- "nessun voto": se la coppia materia,studente non risulta presente
nell'area B3:C12
- La media dello studente nella materia specificata altrimenti.
La soluzione va
costruita utilizzando
le sole funzioni
SOMMA,
MAIUSC,
E,
O,
SE
evitando che appaia l'errore #DIV/0!.
L'uso delle celle di supporto è ammesso.
| ESERCIZIO M1.2.9 |
Si consideri una tabella 5x5 (area B2:F6). Sia Xi,j
il generico elemento posto sulla i-esima riga, j-esima colonna di tale tabella. Costruire una soluzione che verifichi
se
tutti i valori digitati nella tabella "soddisfano" o "non soddisfano" la relazione Xi,j=Xj,i
per ogni i=1...5 e j=1...5.
Suggerimento: utilizzare la funzione
SOMMA,
INDICE
e
SE
e sfruttare gli indici di riga e colonna in figura.
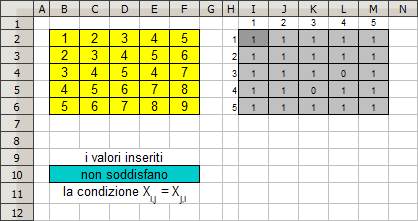
Nella risoluzione le formule di supporto scritte nelle celle grigio chiaro devono essere inserite mediante un'operazione di copia ed incolla partendo dalle celle grigio scuro.
| ESERCIZIO M1.2.10 |
Si consideri una sequenza di 15 numeri digitata
nell'area B3:P3. Fornire una soluzione che restituisca rispettivamente:
nell'area B6:P6 la sequenza riordinata in modo crescente;
nell'area B9:P9 la sequenza riordinata in modo decrescente.
(Suggerimento. usare le funzioni:
PICCOLO
e
GRANDE).
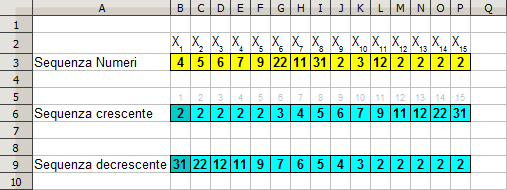
Nella risoluzione occorre considerare che la formula nelle
celle azzurro chiaro devono
essere inserite mediante un'operazione di copia ed incolla partendo dalle celle
azzurro scuro.
| ESERCIZIO M1.2.11 (facoltativo) |
LEGGI: Nel calendario giuliano (promulgato da
Giulio Cesare nell'anno 46 a.C.) un anno è bisestile se il suo numero è
divisibile per 4. Il primo anno bisestile fu il 45 a.C., anno in cui il nuovo
calendario entrò in vigore. Dopo aver assegnato una durata maggiore (si pensa a 445 giorni
al posto dei normali 365) all'anno
708 di Roma (46 a.C.) e che definì ultimus annus confusionis, stabilì che la
durata dell'anno fosse di 365 giorni ma che ogni quattro anni si sarebbe
dovuto intercalare un giorno supplementare. L'anno di 366 giorni fu detto
bisestile perché quel giorno supplementare doveva cadere sei giorni prima delle
calende di marzo (facendo raddoppiare il 23 febbraio) e chiamarsi bis sexto die ante Kalendas Martias (= nel doppio sesto giorno prima delle calende
di marzo). Purtroppo, già nel 44 a.C., subito dopo la morte di Cesare, si iniziò
a commettere errori, inserendo un anno bisestile ogni tre anziché ogni quattro
anni (da un papiro egiziano del 23 a.C. sembra che gli anni bisestili siano
stati: -43, -40, -37, -34, -31, -28, -25, -22, -19, -16, -13, -10). Sarebbe cioè
stata fraintesa l'indicazione di inserire un anno bisestile ogni tre anni
normali, inserendolo invece ogni tre anni compreso quello bisestile (cioè uno
ogni tre invece che uno ogni quattro). Per
rimediare all'errore che aveva già provocato uno sfasamento di 3 giorni Augusto
ordinò che fosse sospesa l'intercalazione del giorno bisestile fino all'anno 4
d.C., che risultò quindi essere il primo anno bisestile dell'era cristiana.
Secondo il calendario giuliano l'anno medio dura quindi
365 giorni e 6 ore. Questa durata non corrisponde esattamente a quella reale
dell'anno solare (ricavata dalle osservazioni astronomiche). Quest'ultimo
infatti è più corto di 11 minuti e 14 secondi. Di conseguenza, il calendario
giuliano accumula un giorno di ritardo ogni circa 128 anni rispetto al
trascorrere delle stagioni.
Per questo motivo nel 1582 fu introdotto il calendario gregoriano,
che riduce l'errore a soli 26 secondi (un giorno ogni 3.323 anni circa).
Con l'attuazione della riforma gregoriana si provvide
anche a correggere gli errori che si erano accumulati nel passato: il
giorno successivo a giovedì 4 ottobre 1582 divenne venerdì 15 ottobre,
attuandosi così un salto di 10 giorni. Fu scelto tale periodo perché in esso non
ricorrevano feste solenni.
Nel calendario Gregoriano un anno è
bisestile se il suo numero è divisibile per 4, con l'eccezione degli anni
secolari (quelli divisibili per 100) che sono bisestili solo se divisibili per
400.
Si potrebbe ulteriormente migliorare il calendario gregoriano togliendo tre
giorni ogni diecimila anni. A tale riguardo John Herschel (1792-1871) suggerì di non
considerare bisestili (mentre, in base al calendario gregoriano, lo dovrebbero
essere) gli anni 4000, 8000 e 12000.
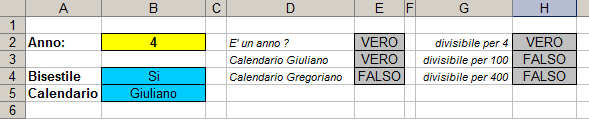
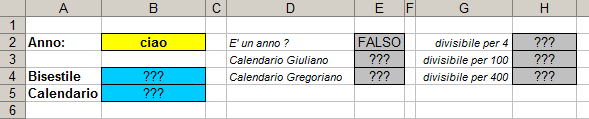
Basandosi sulla precedente lettura costruire un foglio
che accetti in B2 un anno (maggiore di 0) e che mostri se si tratta
di un anno bisestile o meno (usando il calendario in vigore per quell'anno!).
Ad esempio:
- il 900 (Giuliano), il 1300 (Giuliano), il 1896 (Gregoriano) e il 1996
(Gregoriano) sono bisestili;
- il 1582 (Giuliano), il 1997 (Gregoriano) non sono bisestili (non
sono divisibili per 4)
- il 1800 (Gregoriano) e il 1900 (Gregoriano) non sono bisestili (sono divisibili per
4 e 100 ma non per 400);
- il 1600 (Gregoriano) e il 2000 (Gregoriano) sono bisestili (sono divisibili per 400).
Nella risoluzione del problema si suggerisce l'uso di celle di supporto (vedi
figura sottostante) e delle funzioni: =CELLA("TIPO",
Indirizzo), =RESTO(Dividendo,
Divisore), =E(),
=O()
e =NON().
La soluzione deve fornire un meccanismo di
controllo sull'input ed esattamente deve apparire "???"
se non ho scritto l' anno in modo corretto!
Buon Lavoro